[데이터 불러오기]
실습에 사용할 데이터 셋은 1993년 미국의 한 대학에서 공기를 채운 축구공과 헬륨을 채운 측구공을 찼을 때의 거리를 비교하는 실험을 수행한 결과다. 실험은 39회 반복되었으며, 각 시도마다 키커가 공기 및 헬륨을 넣은 공을 교대로 차서 거리를 측정했다.
fba.txt 파일을 복사해서 엑셀에 붙여넣는다.
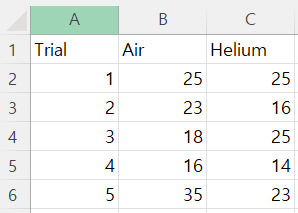
다음과 같이 엑셀에 데이터가 정리된다. 위 데이터의 Trial은 시도 횟수, Air은 공기가 담긴 공의 비행 거리, Helium은 헬륨이 담긴 공의 비행 거리를 나타낸다.
[탐색적 데이터 분석]
본격적으로 통계적 추론에 나서기 이전에 데이터를 살펴보는 탐색적 분석을 수행해보자. 우선 각 시도에 대한 거리의 분포를 살펴볼 필요가 있다. 표와 추세선이 포함된 차트를 그리기 위한 실습 과정은 다음과 같다.

1. 원본 데이터에 표 서식과 조건부 서식을 적용한다. 서식을 적용하면 각 조건 및 시행 횟수에 따른 비행거리 추세를 한 눈에 확인할 수 있다.
2. 데이터의 B열(Air)과 C열(Helium)을 선택한다.
3. 삽입 메뉴에서 꺽은선 차트를 선택하여 차트를 그린다.
4. 차트가 선택된 상태에서 디자인/차트 요소 추가/추세선 메뉴에서 적절한 유형을 선택한다.

5. 선형 유형을 선택하면 다음과 같이 조건에 따른 비행거리를 비교하기 위한 꺽은선 차트가 완성된다. 차트 제목의 경우 더블클릭하여 변경할 수 있다.
이 플롯에서 몇 가지 경향을 관찰할 수 있다.
1. 시도 횟수가 늘어나면서 양쪽 모두 평균 거리가 늘어나는 경향을 보인다. 이는 키커의 학습효과 때문일 것이라고 추정해볼 수 있다.
2. 양쪽 플롯에서 모두 평균에 훨씬 못 미치는 값이 발견된다. 이는 키커의 실수에 기인했을 가능성이 있다.
위 발견을 통계적 추론을 시행하는 데 몇 가지 시사점을 준다.
1. 공의 운동거리는 시도횟수와 양의 상관관계를 갖는다. 따라서 공기와 헬륨 공의 비교에서 시도횟수의 효과를 제거하기 위해서는 각 시도 횟수별 데이터를 묶어서 비교하는 것이 바람직할 것이다.
2. 키커의 실수가 결과에 미치는 영향을 막기 위해 일정 기준에 못 미치는 결과를 제거하고 결과를 분석해야 할 것이다.
[데이터 가공하기]
통계적 추론을 위한 데이터를 준비하도록 하자. 우리가 관심을 갖는 값은 각 시행에서 헬륨과 공기를 채운 공의 운동 거리가 갖는 차이니 여기에 해당하는 속성을 추가하고, 탐색적 분석의 결론을 적용하기 위해 일정 기준에 못 미치는 결과를 제거한다. 실습 과정은 다음과 같다.

1. 각 시행에서 두 공의 운동거리 차이를 구하는 'Differ' 속성을 추가한다.
2. 15야드 이하의 측정값이 포함된 4건의 행을 하나식 선택하여 지운다. 이를 통해 키커가 실수한 부분을 분석에서 제거할 수 있다.

3. 데이터를 제거한 결과는 다음과 같다. 키커의 실수에 해당하는 데이터가 제거된 위 플롯에서는 시행 시기에 따라 꾸준히 거리가 증가하는 트렌드를 좀 더 명확히 관찰할 수 있다.
[통계적 추론]
위 분석 결과를 통해 모집단에 대한 일반화된 결론을 도출해보자. 우선 엑셀에서는 CONFIDENCE.T() 함수를 사용하여 신뢰구간을 계산할 수 있다. CONFIDENCE.T() 함수는 다음과 같은 인자를 필요로 한다.
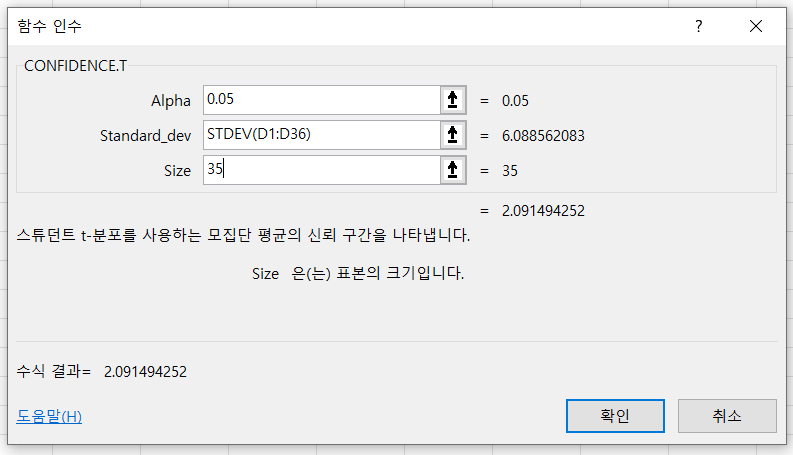
1. 신뢰구간의 넓이: 95%의 신뢰구간을 구하기 위해서는 0.05를 사용한다.
2. 표본의 표준편차: 각 시행별 비행거리의 차이에 대한 신뢰구간을 구하는 것이 목적이므로, 위에서 만든 Differ 속성에 표준편차를 구하는 STDEV() 함수를 적용한다.
3. 표본의 크기: 키커의 실수를 제거한 표본의 크기인 35를 사용한다.
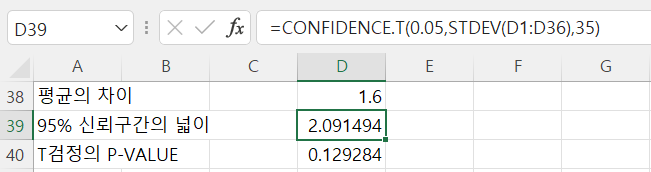
CONFIDENCE.T() 함수가 적용된 결과는 다음과 같다.
다음은 같은 데이터 셋에 대해 가설 검정을 수행한 결과를 알아보자. 엑셀에서는 T.TEST() 함수를 사용하여 두 수치형 속성 간에 유의미한 차이가 있는지에 대한 검정을 수행할 수 있다. T.TEST() 함수는 다음과 같은 인자를 갖는다.
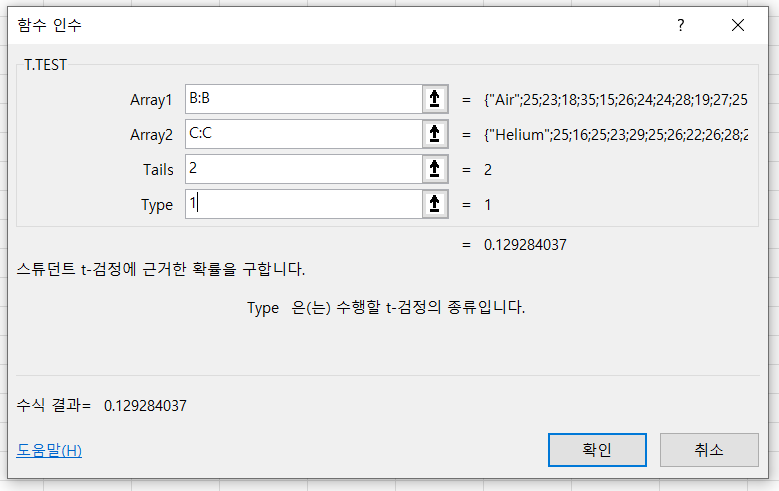
1. 표본 1: 비교 대상이 되는 첫 번째 속성값을 선택한다. 여기서는 Air 속성이 해당된다.
2. 표본 2: 비교 대상이 되는 두 번째 속성값을 선택한다. 여기서는 Helium 속성이 해당된다.
3. 가설 유형: 귀무가설이 '두 속성값에는 유의미한 차이가 없다'고 정의된 경우 2를, 귀무가설이 '한 쪽 속성이 다른 쪽보다 크거나 작다'고 정의된 경우 1을 선택한다. 한 쪽 속성값이 크다는 확신이 없는 한 2를 사용한다.
4. 검정 유형: 각 속성값이 서로 대응되는 경우 1을 선택한다. 그렇디 않은 경우 양 속성의 분산이 서로 일치하는지에 따라 일치할 경우 2, 일치하지 않을 경우 3을 선택한다.
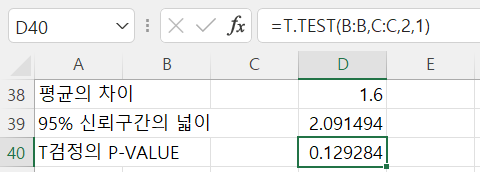
T.TEST() 함수가 적용된 결과는 다음과 같다.
'스터디 > 헬로 데이터 과학' 카테고리의 다른 글
| 엑셀로 해보는 탐색적 데이터 분석 (0) | 2023.08.13 |
|---|---|
| 엑셀을 이용한 데이터 준비 (0) | 2023.08.06 |
| R로 데이터 과학 맛보기 (0) | 2023.07.30 |
| 엑셀로 데이터 과학 맛보기 (0) | 2023.07.30 |



