Lec
[Regression]
Regression toward the mean: 전체 평균으로 되돌아간다.
-> 크거나 작은 데이터가 나와도 결과적으로 전체 평균으로 되돌아가려는 속성을 가진다는 통계적 원리를 의미한다.
[Linear Regression]

y = ax + b
-> 데이터를 가장 잘 대변하는 직선의 방정식을 찾는 것 (기울기와 y 절편을 구함)
[Hypothesis]
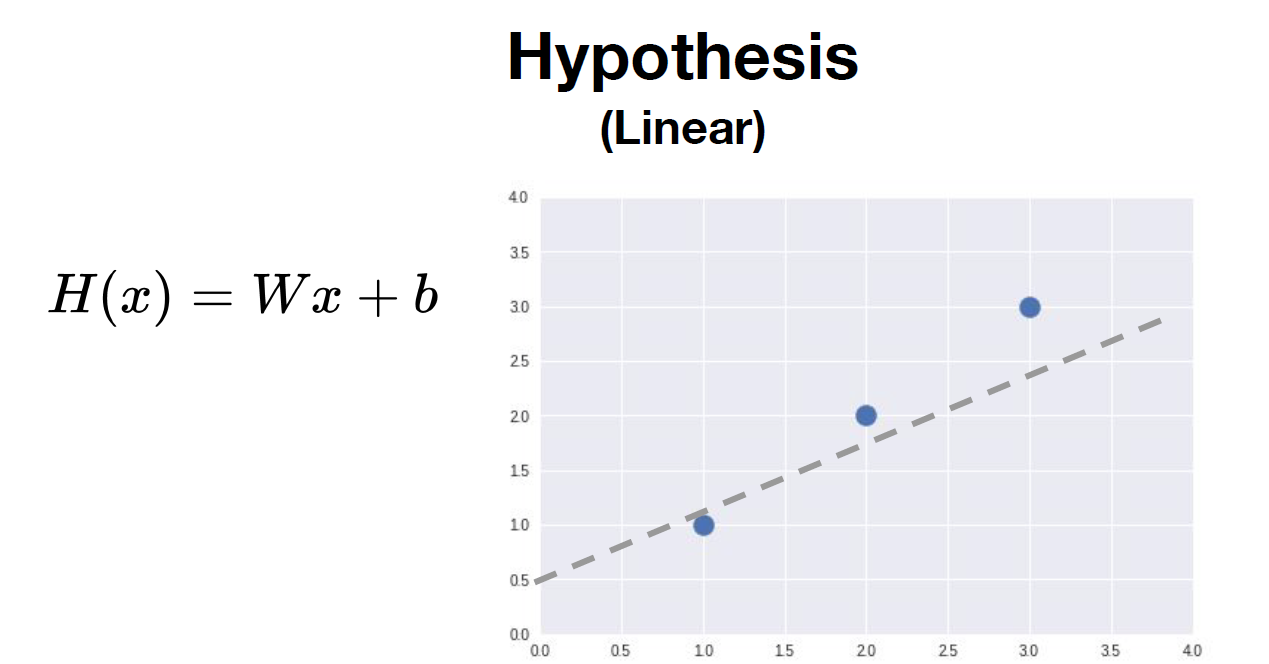
y = ax + b 대신 H(x) = Wx + b로 직선의 방정식을 나타낸다.
[Which hypothesis is better?]
이를 결정하기 위해서는 cost를 생각해야 하는데 이때, Hypothesis를 기반으로 cost를 구한다.
[Cost, Cost function]

H(x) – y
-> 가설과 실제 데이터의 차이
-> 이 값이 작으면 작을수록 데이터를 잘 대변하고 있는 방정식이라 할 수 있다.
-> 양수와 음수의 합을 구하는 것은 무의미하기에 해당 값을 제곱해서 사용한다.
[Goal: Minimize cost]
Cost(W, b)를 최소화하는 W, b를 찾는 것이 목표이다.
Lab
[Hypothesis and Cost]

Hypothesis: H(x) = Wx + b
Cost: H(x) – y의 제곱을 모두 더한 다음 데이터 개수 m으로 나눈 값으로 정의한다.
-> Cost를 최소화하는 W, b 값을 구하는 것을 러닝, 학습이라 말할 수 있다.
[Build hypothesis and cost]


x_data는 input, y_data는 output
-> input의 값과 output의 값이 동일하게 때문에 W와 b의 값이 각각 1과 0이라고 예측할 수 있다.
-> W와 B의 초기값은 임의의 값으로 지정한다.
-> tf.reduce_mean()과 tf.square() 함수를 이용하여 cost function을 TensorFlow code로 정의한다.
[Gradient descent (경사 하강 알고리즘)]

Gradient: 경사, 기울기 / Descent: 하강
tf.GradientTape()는 with 구문과 함께 사용하고, with 구문 안의 변수 변화 정보를 tape에 기록한다.
-> tape의 gradient()를 호출해서 W와 b의 경사도 값을 구한다.
-> learning_rate로 기울기 값을 얼마나 반영할 것인지 결정한다.
-> 이 과정까지 W와 b의 값이 한 번 업데이트 되었다.
[Parameter(W, b) Update]

W와 b의 값이 여러 번 업데이트하기 위해 반복문을 사용한다.
-> W, b의 값이 100번 업데이트 되는 동안 i의 값이 10의 배수가 될 때마다 변화하는 W, b, cost 값을 print
-> W는 1로, b는 0으로, cost는 0으로 수렴하는 결과를 보여준다.
-> 모델이 실제 데이터와 거의 유사하다. (모델이 실제 값을 예측함)
[Training]

학습을 반복하여 W, b의 값을 업데이트 할수록 모델이 실제 값과 유사해지는 모습을 확인할 수 있다.
[Predict]
새로운 데이터를 가지고 예측해보기 (현재 W는 1에 가까운 값, b는 0에 가까운 값)
-> x에 5를 넣은 경우에 실제 결과 값은 5에 수렴하고, x에 2.5를 넣은 경우에 실제 결과 값은 2.5에 수렴한다.
'스터디 > 모두를 위한 딥러닝 시즌 2' 카테고리의 다른 글
| application and tips (0) | 2023.08.06 |
|---|---|
| Softmax Classifier (0) | 2023.08.06 |
| logistic_regression (0) | 2023.08.06 |
| Multi variable linear regression (0) | 2023.07.30 |
| Liner Regression and How to minimize cost (0) | 2023.07.30 |



