Lec
[Simplified hypothesis and Cost]


b를 생략하여 Hypothesis를 간략화 시킨다.
[What cost(W) looks like?]

W의 값에 따라 변화하는 cost의 값을 살펴보기
-> W의 값이 1일 때, cost가 0으로 최소화된 모습을 보인다.
[Gradient descent algorithm]

경사를 따라 내려가면서 최저점을 찾기 위해 경사 하강 알고리즘을 사용한다.
-> 변수의 개수와 상관없이 사용할 수 있는 알고리즘
[How it works? (Gradient descent algorithm의 동작 방식)]
최초의 W, b 값을 정해 최소점에 도달할 때까지 cost가 줄어들 수 있는 방향으로 W, b 값을 지속적으로 업데이트 한다.
[Formal definition]
cost(W, b)을 구하는 과정에서 데이터 m의 개수를 2m으로 바꿔서 사용한다.
-> 계산의 편리함을 위해 바꿔서 사용하는 것이고 cost 값에는 별다른 영향을 주지 않는다.
-> 알파는 기울기 값을 얼만큼 반영할지 결정하는 learning rate를 나타내고, 라운드는 미분 기호를 나타낸다.
[Gradient descent algorithm]
최소점에 도달하기 전까지 W의 값을 지속적으로 업데이트 하는 알고리즘
-> 이전의 W 값에서 (cost function을 미분한 값 * learning rate)의 값을 뺀다.
-> learning rate의 값이 클수록 W의 값이 큰 폭으로 업데이트 된다.
[Convex function]
global minimum: 최저점
local minimum: 주변에서 가장 낮은 지점
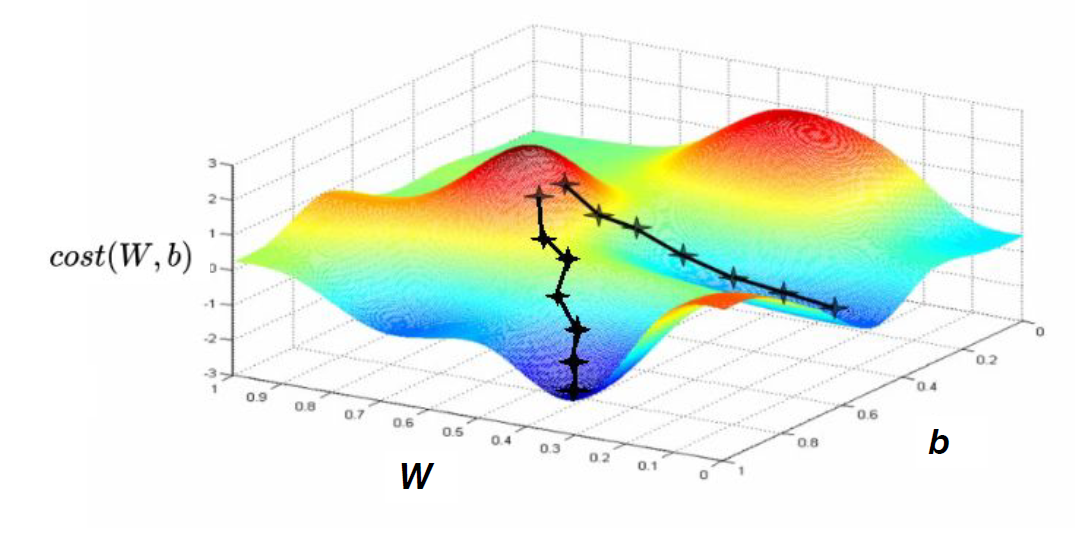
Convex function이 아닌 경우
-> local minimum이 여러 개 존재할 때 local minimum이 최저점으로 도달할 것이라 보장할 수 없다.
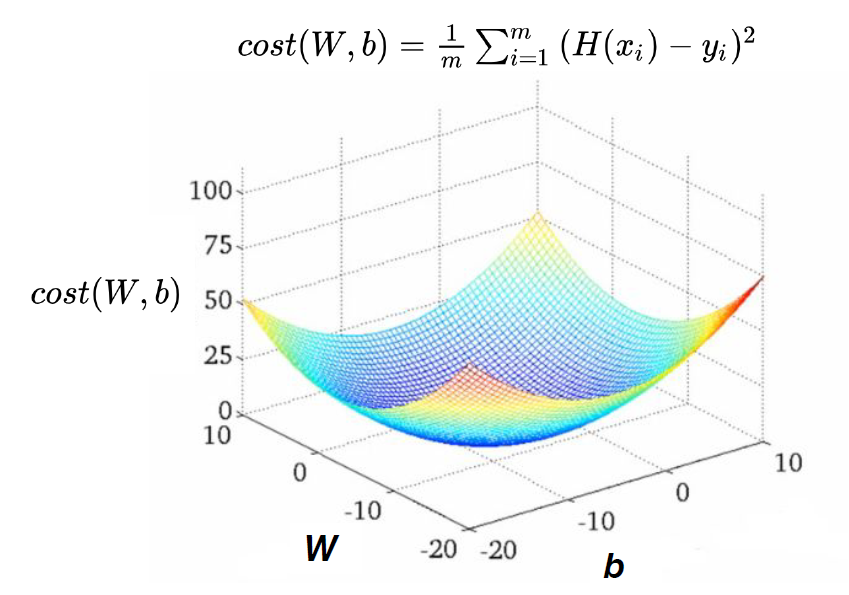
Convex function인 경우
-> global minimum과 local minimum이 같기 때문에 어디에서 시작하든지 최저점으로 도달할 수 있다.
Lab
[Cost function in pure Python]
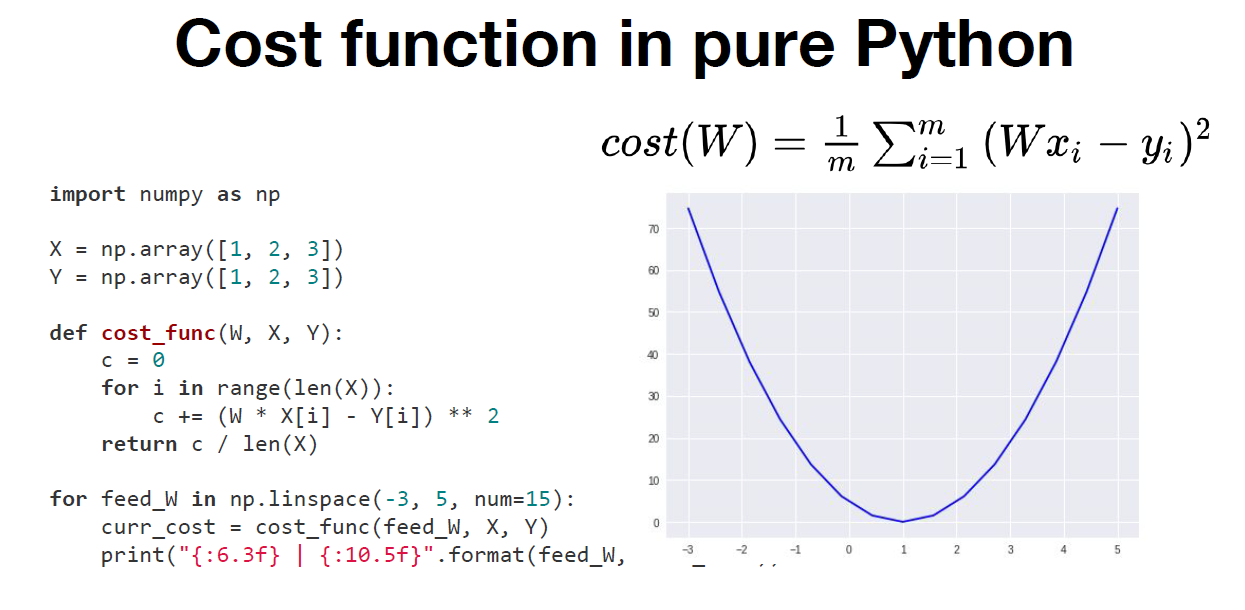
수식을 파이썬 코드로 변환하여 cost_func()로 사용
-> feed_W는 -3과 5 사이를 15개의 구간으로 나뉜 값을 갖게 된다.
-> feed_W의 값에 따라 변화하는 cost 값을 출력한다.
-> W의 값이 1일 때, cost의 값이 최소화 된다.
[Cost function in TensorFlow]
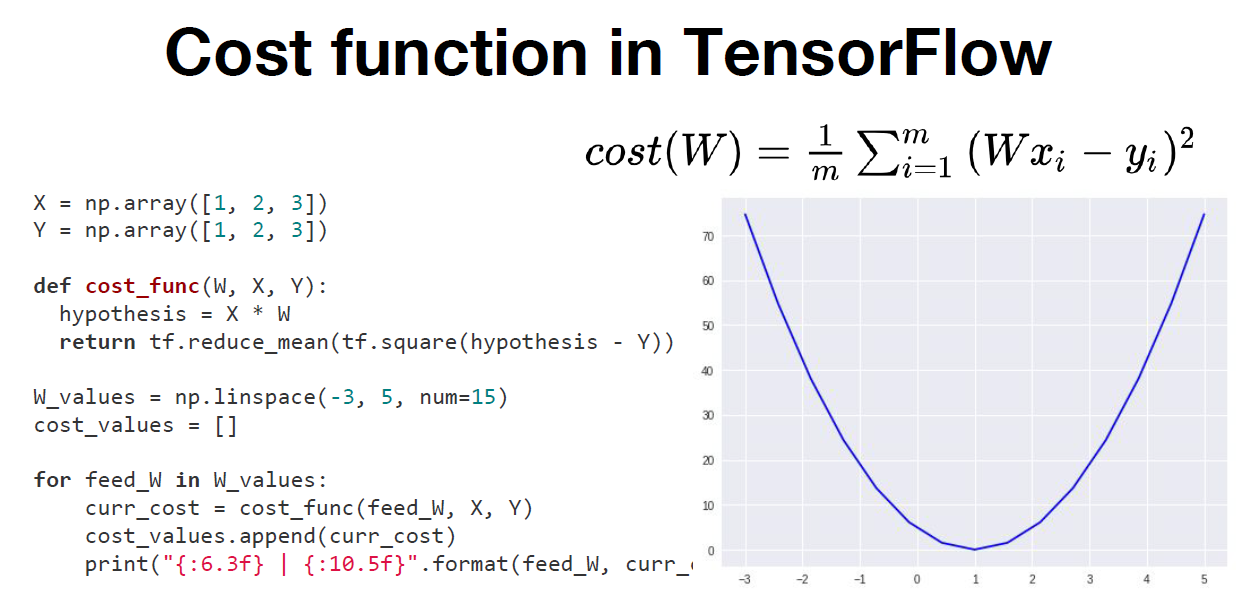
Cost function in pure Python의 모습과 큰 차이점은 없지만 사용하는 함수가 다르다.
[Gradient descent]

Gradient descent를 TensorFlow code로 변환한다.
-> tf.set_random_seed(0)으로 random_seed을 초기화 한다.
-> 정규분포를 따르는 random_normal로 W의 값을 임의로 지정한다.
-> 업데이트 된 W의 값을 descent에 저장한 다음 W.assign() 함수를 통해 W의 값을 새로 할당한다.
-> cost의 값은 0으로 수렴하고, W의 값은 특정한 값으로 수렴한다.
[Output when W=5]

W의 값을 random이 아닌 특정한 값인 5로 지정했을 때에도 같은 결과를 보여준다.
'스터디 > 모두를 위한 딥러닝 시즌 2' 카테고리의 다른 글
| application and tips (0) | 2023.08.06 |
|---|---|
| Softmax Classifier (0) | 2023.08.06 |
| logistic_regression (0) | 2023.08.06 |
| Multi variable linear regression (0) | 2023.07.30 |
| Simple Liner Regression (0) | 2023.07.30 |



